[DL] Cross-Entropy 이해하기

카테고리 없음

[DL] Cross-Entropy 이해하기

meenham 2024. 7. 17. 18:40

1. 요약

- cross-entropy 의 식은 아래와 같다.

- 의미 : 확률분포 P, Q 의 차이를 나타낸다.

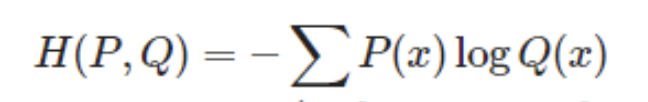
- 내용1 : 수식이 왜 위와 같은 형태를 띄는가

1) 정보량

2) 엔트로피

- 내용2 : 수식은 어떻게 두 분포의 차이를 드러내는가

- 내용3 : 분류 문제에 MSE 대신에 cross-entropy 를 적용하는 이유

2. 정보량

- 정보량이란 무엇인가?

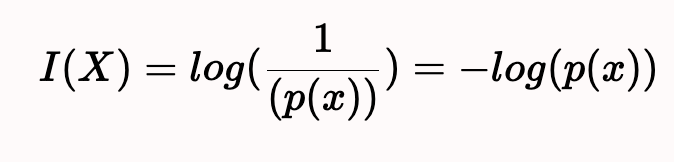
1) 직관적 설명

- 놀람의 정도, 발생 확률

- 사건의 발생 확률이 낮을수록, 놀람의 정도는 높아지기에, 사건은 높은 정보량을 갖고 있다고 할 수 있다.

2) 정보이론을 통한 설명 ( 해당 설명은 서동해님의 블로그를 인용합니다, 너무 완벽해서 더 잘 정리할 수가 없습니다. ) ( https://blog.naver.com/gypsi12/222952809693 )

- 세상에는 많은 종류의 정보가 있다.

- 이들을 하나의 기준으로 표현하고자 한다.

https://blog.naver.com/gypsi12/222952809693

예시는 다음과 같다.

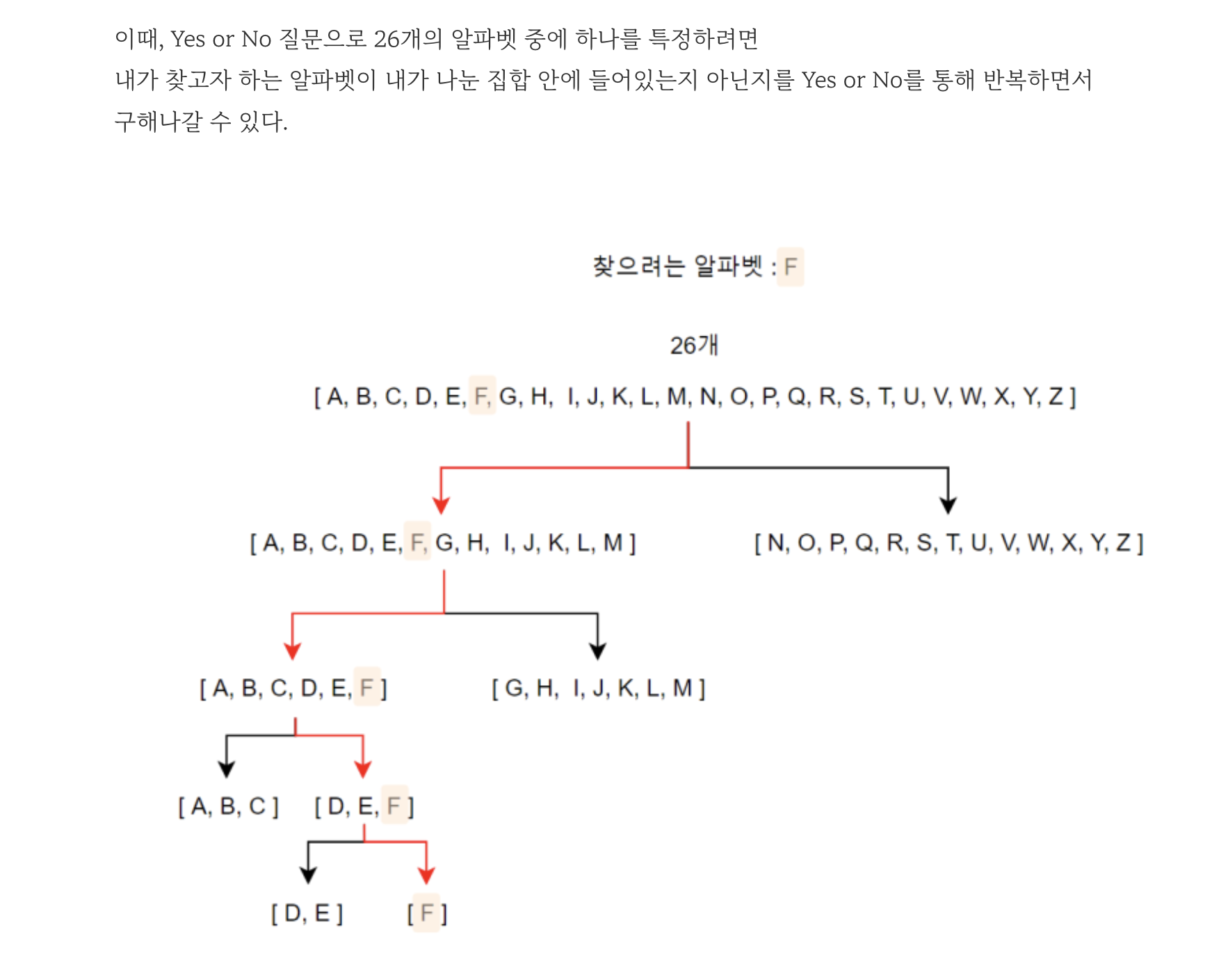
정보량을 구하는 식

3. 엔트로피

- 정보량 : 하나의 사건에 대한 놀람의 정도, 질문의 개수를 나타낸다.

- 엔트로피의 경우, 어떤 사건에 대한 확률분포의 정보량을 의미한다.

- 즉, 사건을 표현하기 위한 평균 정보량이다.

- 정보량에 대해 기댓값을 취하면 된다.

- 즉, 각 사건의 정보량 I(x) 에 정보가 등장할 확률 p(x) 를 곱해주고, 모두를 더해주면 된다.

https://esj205.oopy.io/12ffe440-5ebf-465a-bf7b-aae4db855fa7

- uniform 한 분포일수록 엔트로피 값이 크다.

- 예측이 어려울수록 평균 정보량이 더 커진다.

- 즉, 불확실성의 개념으로 이해하면 쉽다.

< 엔트로피의 최댓값과 최솟값 >

1) 확률변수가 결정론적이면, 확률분포에서 특정한 하나의 값이 나올 확률이 1이다. 이때 엔트로피는 0이 되고, 이 값은 엔트로피가 가질 수 있는 최솟값이다.

2) 반대로 엔트로피의 최대값은 이산확률변수의 클래스의 갯수에 따라 달라진다. 만약 이산확률변수가 가질 수 있는 클래스가 2^k 개 이고, 이산확률변수가 가질 수 있는 엔트로피의 최대값은 각 클래스가 모두 같은 확률을 가질 때이다. 이때 엔트로피의 값은 H= - 2^k/2^k * log(1/2^k) = k 이다.

3. 수식은 어떻게 두 분포의 차이를 드러내는가?

- entropy 식과 cross-entropy 식

- log 내부의 p(x) 를 q(x) 로 대체함으로서 갖는 수학적 의미에 대해 이해하지 못했다. 서동해님의 블로그에서 https://blog.naver.com/gypsi12/222952809693 이를 다루는 부분이 있는데, 잘 와닿지 않았다. 궁금하신 분들은 들어가서 읽어보시길 바랍니다.

- 다만, log 내부의 p(x)를 q(x) 로 대체했을시에, 결과값이 어떤 기능을 할 수 있는지에 대해서는 이해할 수 있었다.

- 이해한 흐름을 다음과 같이 간략하게 정리할 수 있다.

1) (KL-Divergence) = ( cross-entropy ) - ( entropy ) >= 0

<=> ( KL-Divergence ) = H[P,Q] - H[P,P] >= 0 ( P, Q 는 확률분포 ; H는 엔트로피 )

2) 딥러닝에서 P는 정답 확률분포, Q는 예측 확률분포 이다. 즉, P는 고정값, Q는 변동값 이다.

3) Q 분포가 P 분포에 가까워질수록, ( KL-Divergence ) 값이 작아질 것이다.

4) 따라서 KL-Divergence 를 최소화시키는 과정은, Q 분포를 P 분포에 가깝게 만드는 과정과 동일하다.

5) H[P,P], 고정된 P 분포 하의 엔트로피 값, 는 상수값이기 때문에 KL-Divergence 를 최소화시키는 과정은, Cross-Entropy를 최소화시키는 과정과 동일하다.

6) 위 과정을 통해 엔트로피 식에서 log 안의 p(x)를 q(x)로 대체했을 시의 결과값은 이전의 값보다 크다는 사실을 알 수 있고,

7) q(x) 분포를 p(x) 분포로 수렴시키는 과정이 결과값을 최소로 감소시키는 과정임을 알 수 있다.

8) 따라서 log 안의 p(x)를 q(x) 로 대체하는 과정이, 두 분포의 차이를 계산하는 과정이라고 이해할 수 있다.

- KL-Divergence 값이 0 이상인 이유는, 다음의 블로그에 잘 정리되어 있다.

https://hsm-statistics.tistory.com/169

[KL divergence 의 이해] 5. KL divergence 왜 항상 0보다 같거나 큰가 (증명)

KL divergence 는 아래와 같이 정의됩니다. $D_{KL}(p||q)=H[p,q]-H[p]$ 크로스엔트로피와 엔트로피의 차이입니다. 수식을 자세히 쓰면 아래와 같습니다. $D_{KL}(p||q)=\int_{-\infty}^{\infty}p(x)\ln \frac{p(x)}{q(x)}dx$

hsm-statistics.tistory.com

3. 분류 문제에 MSE 대신에 cross-entropy를 적용하는 이유

1) 회귀 문제에는 MSE 를 주로 이용한다.