[NLP] Word Embedding : GloVe

해당 블로그의 내용은 다음의 링크를 정리하여 작성한 내용입니다.

 

- reference : https://wikidocs.net/22885

09-05) 글로브(GloVe)

 

Glove ( Global Vectors for Word Representation )

- 2014년 스탠포드 대학에서 개발

- 카운트 기반의 LSA 와 예측 기반의 Word2Vec 의 단점을 지적하며 이를 보완한다는 목적으로 나왔다.

- Word2Vec 만큼 뛰어난 성능을 보여준다.

- Word2Vec 과 Glove 중에 어떤 것이 더 뛰어나다고 말할 수 없고, 이 두 가지 전부를 사용해보고 성능이 더 좋은 것을 사용한다.

- Word2Vec 과 함께 가장 많이 쓰이는 단어 임베딩 기술이다.

 

- Word2Vec은 자주 사용되는 단어가 있으면, 그 단어에 대해서 너무 많이 계산한다는 것이다.

- 이를 원천적으로 해결하기 위해 등장한 방법이다. 

 

- 아이디어 : 임베딩 된 중심 단어와 주변 단어 벡터의 내적이 전체 코퍼스에서의 동시 등장 확률이 되도록 마드는 것. 즉, 이를 만족하도록 임베딩 벡터를 만드는 것이 목표이다. 

 

 

GloVe 의 손실함수를 설계하기 위해서는 동시 등장 행렬과 동시 등장 확률을 이해해야 한다.

 

1. 윈도우 기반 동시 등장 행렬

동시 등장 행렬은 다음의 특징을 지닌다.

- 행과 열을 전체 단어 집합의 단어로 구성한다.

- i 단어의 윈도우 크기 내에서 k 단어가 등장한 횟수를 i행 k열에 기재한 행렬이다.

- 예제를 보자

 

2. 동시 등장 확률

- 동시 등장 확률 P(k|i) 란, i가 등장했을 때, 어떤 단어 k가 등장한 횟수를 계산한 조건부 확률이다.

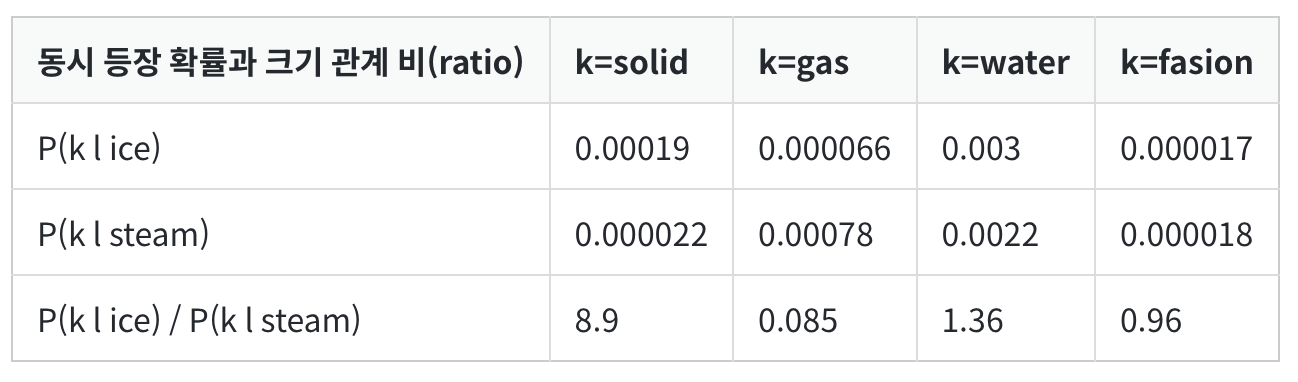
해석 

- ice가 등장했을 때, solid가 등장할 확률은 0.00019 이다. stream 이 등장했을 때, solid가 등장할 확률은 0.000022 이다. 무려 8.9배 ice가 함께 많이 등장한 것이다. '단단한' 의미를 가진 solid 는 '증기'라는 의미를 띄는 steam 보다는 '얼음' 이라는 의미를 지닌 ice 와 연관이 되어 있기 때문일 것이다. 

- 1에 가까운 경우는 관계가 비슷하다고 할 수 있을 것이다.

- 이를 조금 더 보기 쉽도록 단순화하면 다음의 표로 나타낼 수 있다.

 

자 이제, 동시 등장 행렬과 동시 등장 확률의 이해를 바탕으로 손실 함수를 설계해보겠습니다.

 

손실 함수 ( Loss function )

- 용어 정리

 

- GloVe 아이디어 : 임베딩 된 중심 단어와 주변 단어 벡터의 내적이 전체 코퍼스에서의 동시 등장 확률이 되도록 만드는 것

- 이를 만족하도록 임베딩 벡터를 만드는 것이 목표이다.

- 이를 식으로 표현하면 다음과 같다.

 

- 더 정확히는 log 함수를 이용하여 임베딩 벡터를 설계하게 된다.

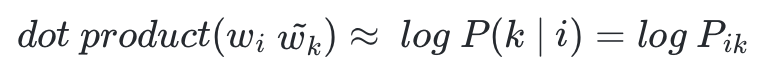
- 임베딩 벡터를 만들기 위해 손실함수를 처음부터 차근히 설계해보자

- 가장 중요한 것은 단어 간의 관계를 잘 표현하는 함수여야 한다는 것이다

- 하나의 단어를 고정시키고, 두 단어와의 관계를, 동시 등장 확률을 이용하여 표현하도록 한다.

- 다음의 식으로서 전개를 시작한다.

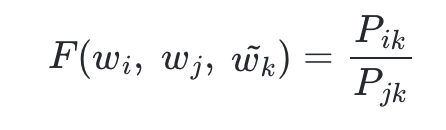
- 아직 함수 F 가 어떤 식을 가지고 있는지는 정해진 바가 없다.

- 최적의 식에 다가가기 위해 디테일을 추가해보자

- 함수 F 는 두 단어 사이의 동시 등장 확률의 크기 관계 비 정보를 벡터 공간에 인코딩 하는 것이 목적이다. 

- 이를 위해 GloVe 연구진들은 wi, wj 두 벡터의 차이를 함수 F 의 입력으로 사용하는 것을 제안한다.

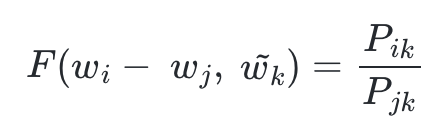
- 여기서 좌변은 벡터값이고, 우변은 스칼라 값이다. 이를 성립해주기 위해 함수 F 의 두 입력에 내적을 수행한다.

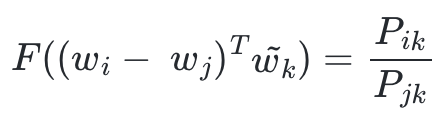
- 정리하면, 선형 공간에서 단어의 의미 관계를 표현하기 위해 뺄셈과 내적을 택했다.

 

여기서 F 가 만족해야 할 필수 조건이 있다.

- 중심 단어와 주변 단어 w 라는 선택 기준은 실제로는 무작위 선택이므로, 이 둘의 관계는 자유롭게 교환될 수 있어야 한다.

- 이것이 성립되게 하기 위해 GloVe 연구진은 함수 F가 실수의 덧셈과 양수의 곱셈에 대해 준동형(Homomorphism)을 만족하도록 한다.

- 식으로 나타내면 다음과 같다.

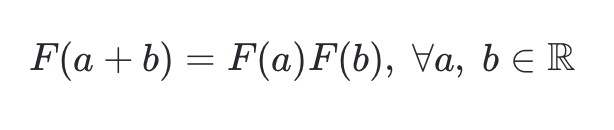
- 이 준동형식을 현재 전개하던 GloVe 식에 적용할 수 있도록 바꿔보자

- 함수 F의 결과 값으로는 스칼라값이 나와야 한다.

- a,b가 각각 벡터값이라면 함수 F의 결과값으로 스칼라 값이 나올 수 없지만, a,b가 사실 두 벡터의 내적값이라고 하면 가능하다.

- 따라서 위의 준동형식을 아래와 같이 바꿔보겠다.

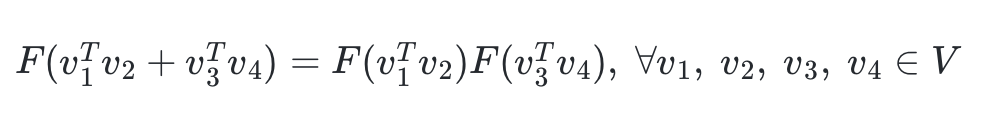
- 앞서 작성한 식에서 wi, wj 두 벡터의 차이를 입력으로 받았다. 그렇게 되면 곱셈도 나눗셈으로 바뀌게 된다.

- 이전 식에 따르면 우변은 본래 P(ik)/P(jk) 였으므로, 결과적으로 다음과 같다.

- 좌변을 풀어쓰면 다음과 같다.

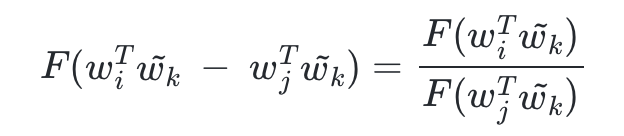
- 이를 만족하는 함수 F를 찾아야 한다.

- 그리고 이를 정확하게 만족시키는 함수가 있는데, 바로 지수 함수 이다. 

- F를 지수함수 exp 라고 해보자.

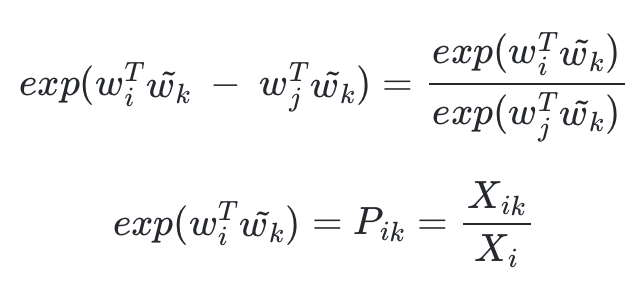
- 위 두번째 식으로부터 다음의 식을 얻을 수 있다.

- wi, wk 는 두 위치를 서로 바꾸어도 식이 성립해야 한다.

- Xik 의 정의를 생각해보면 Xki와도 같다.

- 그런데 이게 성립되려면 위의 식에서 log Xi 가 걸림돌이다.

- 이 부분만 없애면 성립시킬 수 있다.

- 그래서 GloVe 연구팀은, log Xi 항을 wi 에 대한 편향 bi 라는 상수항으로 대체하기로 한다. 

- 같은 이유로 wk 에 대한 편향 bk 를 추가한다.

- 이 식이 손실 함수의 핵심이 되는 식이다.

- 우변의 값과의 차이를 최소화 하는 방향으로 좌변의 4개의 항은 학습을 통해 바뀌는 변수가 된다.

- 즉, 손실 함수는 다음과 같이 일반화 될 수 있다.

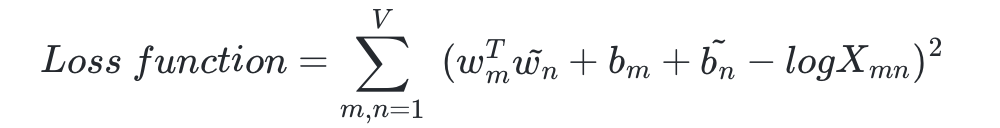
- 여기서 V 는 단어 집합의 크기이다.

- 아직 최적의 손실 함수 라기에는 부족하다.

- log Xi 에서 Xi 가 0 이 될 수 있음을 지적한다.

- 대안 중 하나는 log Xik 항을 log (1+Xik) 로 변경하는 것이다.

- 하지만 이렇게 해도 해결되지 않는 문제가 있다.

 

- 바로 동시 등장 행렬 X 가 희소 행렬 (sparse matrix ) 일 가능성이 다분하다는 점이다.

- 많은 값이 0 이거나, 작은 수치를 갖는 경우가 많다.

- 이에 대한 가중치를 주는 고민을 하게 되는데, 바로 Xik 의 값에 영향을 받는 가중치 함수 f(Xik)를 손실 함수에 도입하는 것이다.

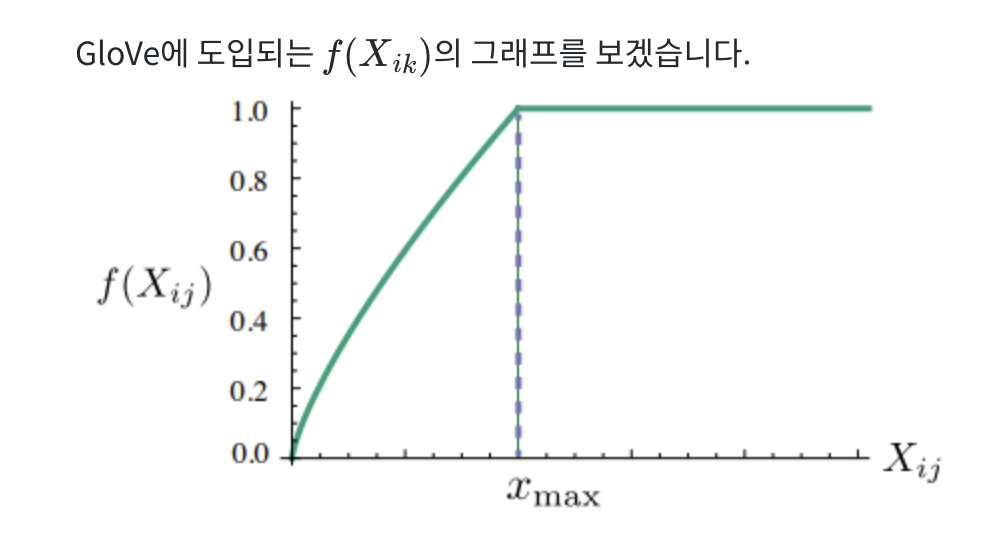
- GloVe 손실 함수에서 사용하는 가중치 함수는, 동시 출현 빈도가 높은 단어 쌍에 높은 가중치를 부여하고, 낮은 단어 쌍에 낮은 가중치를 부여하는 것이다.

- 하지만 Xik가 지나치게 높다고 해서 지나친 가중치를 주지 않기 위해서 함수의 최대값이 정해져 있다. 최대값은 1

- 최종 손실 함수는 다음과 같다.